Dragon
Dragon. Spray + Acrylic on canvas. Stencils built using a CNC shopbot.
A Clojure DSL for Web-Crawling
When building crawlers, most of the effort is expended in guiding them through a website. For example, if we want to crawl all pages and individual posts on this blog, we extract links like so:
- Visit current webpage
- Extract pagination links
- Extract link to each blog post
- Enqueue extracted links
- Continue
In this blog post, I present a new DSL that allows you to concisely describe this process.
This DSL is now part of this crawler: https://github.com/shriphani/pegasus
A Frame That Listens
The incredibly talented Pem Lasota, Aram Ebtekar and I put together a small project to enhance the music experience in our living room.
What ensued is the first of many projects we plan to roll out - all focused on building the greatest living-room music experience in the world.
The setup involves 4096 LEDs arranged in a matrix, powered by a raspberry pi and a beefy condenser mic. The electronics fit into a 3D printed case. Pem did a significant chunk of this in Solidworks - a piece of software I was extremely impressed with. In one of the sessions, I was able to make reasonable headway with mild supervision. Few pieces of software are this easy to pick up. Solidworks have done a solid job.
and when everything is put together, it looks like this:
The frame listens via the condenser mic and generates beautiful visualizations when it “hears” audio. This is what happens when we blast Pavarotti on our music system:
A neutrino effect to Flume's Hyperparadise:
The Matrix effect when the bass drops:
The Lunacy of The Apple India Story
In India, 30% of goods sold by foreign companies must be manufactured within the country.
This law puts a damper on Apple’s India plans - threatening to prevent them from bringing their incredibly successful retail strategy to the country.
Turns out there’s an exemption for retailers providing cutting-edge technology. Apple apparently failed to qualify for this exemption. This decision is top-level comedy coming from a country that has failed to deliver indoor plumbing to more than half its citizens.
There’s a beautiful anecdote from the 80s or 90s (or some other time the nation was conducting its large-scale economics-voodoo social experiments). Sunil Mittal - founder of Airtel, one of India’s largest telecom companies - saw a push-button phone on a trip in Taiwan and decided to bring it to India - where the rotary dial was still state-of-the-art.
Turns our phone imports were banned. The burgeoning company had to set up operations to buy fully built phones in Taiwan, break them apart, ship them to India, and then reassemble them.
I am sure that this lunacy was fully paid for by the customers.
Sunil himself mentions this story near the 16:25 mark:
If you wondered where to look for a Yakov Smirnoff jokes in a post Soviet world, India’s got your back.
India’s vast bureaucracy is now bringing its finely honed judgement to deal with the world’s most successful companies.
fort-knox: A disk-backed core.cache implementation
core.cache is a small and convenient cache library for clojure. It enables clojure users to quickly roll out caches. In this blog post I am going to describe a clojure implementation which stores cache entries to disk: fort-knox.
In a few recent projects I’ve needed a cache with entries backed to disk. This is a vital requirement in applications that need to be fault-tolerant. LMDB (which I’ve had very positive experiences with) is fast, quick and perfect for this task. fort-knox implements the core.cache spec and stores entries in LMDB. clj-lmdb (subject of a previous blog post) is part of the plan now.
Note that this library deviates slightly from suggestions for core.cache implementations. For instance, the backing store doesn’t implement IPersistentCollection or Associative so fort-knox might deviate from expected behavior. Thus YMMV.
Consuming News: 2016
Quartz has a new news app - an absolute peach.
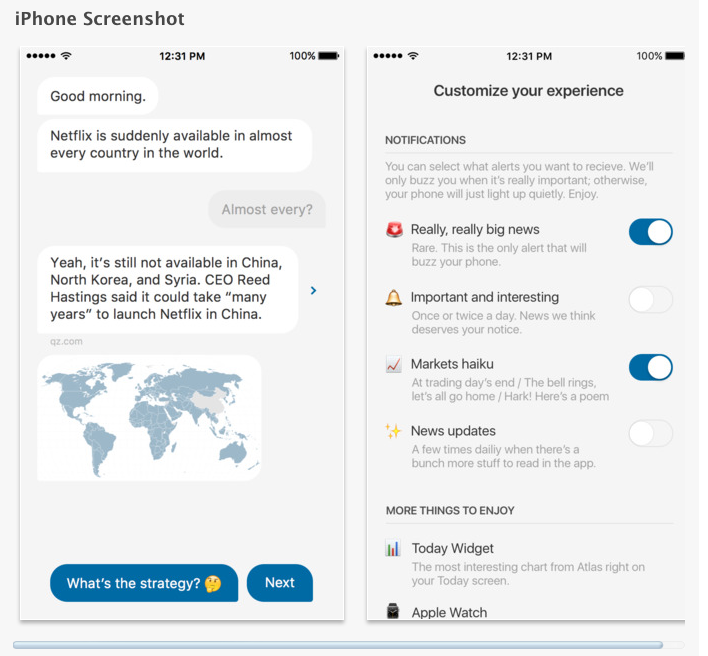
The NYTimes in comparison is a brain-dump.
As a kid, in the pre-WWW days, people around me consumed news in the following forms (I couldn’t be bothered):
- 30 minute segments thrice a day on a popular TV network.
- Newspaper covering stuff from a time-period between last week and 2:00 am this morning.
- 24 hour news on TV.
The WWW presented a challenge (and still does) for traditional news orgs. I believe all content gets 2 kinds of eyeballs - the kind of folk who are looking for exactly that content and the kind who are bored and will watch whatever is on. When a TV producer sets up a narrative for a day’s worth of programming, you get the attention of both these groups - there are few other options.
In an on-demand world, long-form news that is hastily put together needs to compete with youtube videos, reddit and so on. Converting a narrative of events into a blob of text you can put on your site is going to attract only the kind of people who want to read this sort of stuff in their spare time.
In my experience this species loves the color beige and has the world-view of prep-school headmasters.
And to capture and lock down this audience, you are forced to convert journalism into a weird vaudeville performance. In fact The Daily Show ended up becoming a meta-news org making fun of this phenomenon.
As print journalism and 24 hour news orgs die, I see 2 main vehicles for news consumption emerging:
- Breaking news outside traditional media cycles - plane crashes, etc. This is stuff that will go viral on social media before a reporter arrives at the site.
- Breaking news within traditional media cycles. A presidential candidate’s decision to drop out of a race will typically be leaked to the NYTimes or some other established organization.
- A stream of news delivered thrice a day - possibly personalized since people don’t enjoy their senses being assaulted with information all the time. The new Quartz app (I think) fits this space nicely. The NYTimes has an app called NYTNow but it isn’t clear to me if the feed is personalized at all. Given that the service has a twitter presence, it is entirely possible that there is zero personalization.
- Long form analysis with amazing visualizations. This sort of stuff requires expertise along several dimensions - something I’ve seen the NYTimes excel at. They produced this brilliant piece on school districts, this exceptional piece on Michael Bloomberg’s tenure as mayor and this beautiful piece on the silk road.
This leaves us with how to make $$.
I don’t think breaking news is a serious vehicle to make money (anymore). However existing media shops need to invest in this space to maintain an aura of legitimacy. This might change in the future but today’s expectations of a news org include breaking news. It might be ok for a newer media org to become purely an analysis-based-reporting organization (like Nate Silver’s http://fivethirtyeight.com/), but I would still like the news app to alert me when something serious happens (like the Paris attacks) and not have to discover this on Twitter.
Quartz has been delivering small ads in the news stream that look like this:
I like these sorts of ads - they aren’t intrusive (well, for now) and possibly get you more impressions than whatever the status quo is.
There are 2 additional examples I want to cover. TomoNews is an incredibly creative news org. The animated shorts are rather entertaining.
BuzzFeed has mastered the art of bringing people to their site, creating a stable revenue stream from their baity content and produce some very nice long-form news articles.
To survive, journalism needs to change. There are new gatekeepers, new platforms and new competitors. News needs to change from a brain-dump to a new kind of performance art. Existing media powerhouses have several weapons in their war chest - a brand-name that resonates well, existing relationships with the rich and powerful, and revenue streams (they might be dwindling but at least they’re around).
This soft-power needs to mix with the best photography, web-design, typography and visualization-tech. Each piece of investigative journalism should become a distinct, pleasant memory - like when Walter Cronkite covered the moon landings:
In short, give people something they will enjoy for a reasonable price.
Carrots And Sticks: The Semantic Web
In 2014 I attended a talk by Ramanathan V. Guha on schema.org. Its remarkable adoption offers several lessons about building internet properties.
Schema.org is an ontology - a vocabulary for annotating HTML documents with information. For instance, you can put in some info in the web-page markup stating that what you’re displaying is blog post or a list of products.
For instance, a website can present its content and state that this content is an instance of Blog (say). Schema.org is a central repository describing what Blog is, what and where it fits in an ontology.
As of 2015, Schema.org is by far the most dominant vocabulary used on the internet [1].
Schema.org accomplished this feat by aligning incentives correctly. First, annotated webpages would result in a richer search-result presentation - translating to better traffic to the website - a massive economic incentive. Next, the top 4 players in search agreed to support Schema.org - Google was obviously the mothership, bing, Yahoo and Yandex supported it.
Schema.org offers an amazing lesson in setting up the incentives correctly. When you’re building a standard, waiting for people to adopt your rules on the basis of their merit is slightly less efficient than not building the standard at all. A clear economic incentive is a powerful motivator.
The Schema.org team understood that well. And now there is an amazing foundation that is being exploited by a new generation of applications.
clj-lmdb : Clojure Bindings For The LMDB Key-Value Store
LMDB is the nicest, no-nonsense, no-surprise key-value store I’ve ever used.
In several benchmarks, LMDB destroys competitors - it is a beloved tool in high-profile circles.
Here’s clojure bindings: https://github.com/shriphani/clj-lmdb
Genius
One of the more memorable courses I took at Carnegie Mellon was Manuel Blum’s algorithms.
The CSD made it a mandatory course for some major (I don’t know about this since I was just fucking around for the most part).
It is a little known secret that you don’t attend Manuel’s course to learn about algorithms - you can learn quite well by opening a book.
You attend to watch a genius combine expertise, brilliance, and passion.
When I took the course, Manuel wanted to get up to speed with machine learning. As of 2014 Manuel had won the Turing award, his students shared among them three Turing awards, founded new fields in computer science like Quantum Computing, and founded successful companies which went on to become cultural phenomena - ReCaptcha and Duolingo among them.
Manuel’s course essentially involved delivering a lecture on a topic of your choice - I made a proper horlicks of my talk. However, it inspired a lively blog post and visualization here.
I was pretty excited to meet Manuel in person. Back in high school I was avid follower of Scott Aaronson’s blog and he spoke highly of his advisor Umesh Vazirani. Manuel was Umesh’s advisor and it was a meeting-your-childhood-hero moment for me.
From the entire course, two things stood out:
- Manuel is incredibly hard to lecture to. This is not a criticism, it is a harsh reminder that most academic talks are pathetic. Manuel placed immense emphasis on getting the axioms, the aphorisms and the fundamentals right. Opening a talk like you open an abstract was a sureshot way of getting asked a question two sentences in.
- Manuel engaged heavily with students. Prior to World War II, a student was evaluated based on an oral examination by their instructors. My colleagues at work who were educated in Europe mention that this tradition is being preserved across the pond. Manuel believed in this interaction - education for him was a socratic dialogue.
- Manuel randomly sampled material from tons of books - a technique that broadened his expertise and world-view immensely.
Manuel has tons of amazing advice for students on his website. Personally, when I took his course, due to a variety of circumstances, I had mentally checked out of CMU.
Manuel was the display of intellect I needed to not descend into deep cynicism about a life devoted to learning.
Human Athleticism Never Ceases To Amaze
#KeepPounding #Panthers #SB50 Super Bowl 50: Broncos vs. Panthers CBS https://t.co/BwlJmzjPlX pic.twitter.com/iNWUm6lgWs
— ClippitUsers Sports (@FanSportsClips) February 8, 2016
Twitter: @shriphani
Instagram: @life_of_ess
Fortior Per Mentem
(c) Shriphani Palakodety 2013-2020